The Case for Sparse Pattern Based Bayesian Neural Networks
The overconfidence of DNNs has attributed to the recent trend towards stochastic machine learning with uncertainty quantification becoming an important requirement across many different tasks. As stated, the ability for a network to give an interpretation and provide statistical insights of its predictions is critical across numerous application domains.
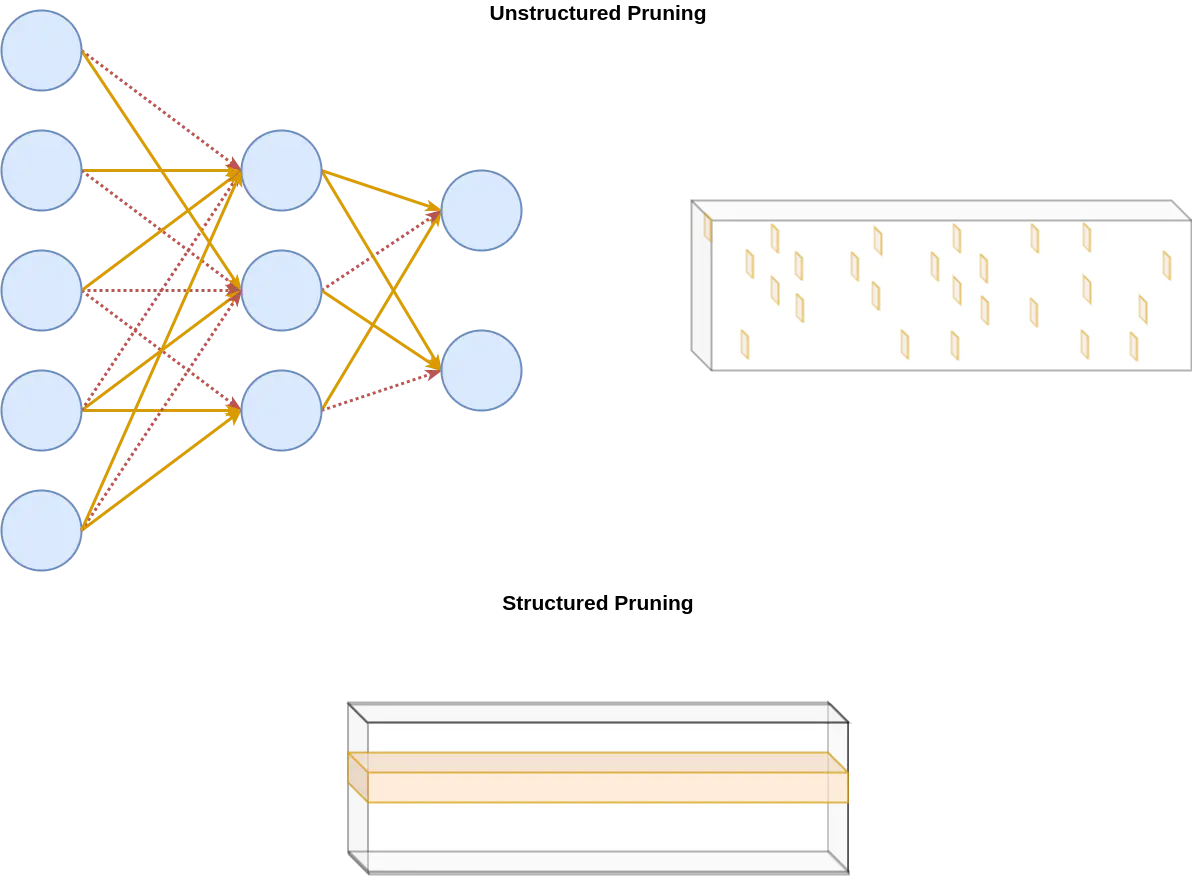 Image credit: Adam Ghanem
Image credit: Adam GhanemOver a period of time, deep neural networks (DNNs) have spiralled further and further into more complex and elaborate systems, desiring huge amounts of data and computational power for sustenance. These networks have grown to supersede human level performance across a wide range of applications with a high level of accuracy. Recent breakthroughs by Tan and Le [60] realise substantial performance improvements while reducing the amount of computation required for DNNs. DNNs have also seen their rise to prominence in fields such as medical diagnosis and self-driving cars [29, 31]. A plethora of industries are being slowly aided or replaced by artificial intelligence systems and there is a growing responsibility to ensure the validity and quality of their predictions.
With this success comes a number of shortcomings, specifically with rectified linear unit (ReLu) based neural networks, where researchers question how confident these models are in their own predictions and hence their suitability in critical domains [24]. This uncertainty is a statistical property that is pivotal to measure and analyse across a wide range of domains, from scientific analysis, self-driving cars to medical diagnosis. The overconfidence of these models could very well cause devastating vehicular accidents or even botched medical procedures and recommendations. One such example of the dangers of disregarding uncertainty estimation is already coming to light through social issues [47] which details the rise in digital awareness for policing systems. The implications of an artificial intelligence (AI) policing system have raised significant questions on the suitability of these models in making predictions that take sensitive factors into account to help prevent prejudice against race, community, health, affluence and a variety of other factors.
The overconfidence of DNNs has attributed to the recent trend towards stochastic machine learning with uncertainty quantification becoming an important requirement across many different tasks. As stated, the ability for a network to give an interpretation and provide statistical insights of its predictions is critical across numerous application domains. The growing interest has led to a variety of stochastic methods that have been leveraged to provide a different approach to the standard deep or convolutional neural network (CNN), which is essentially a regularised version of a standard fully-connected network used for image classification tasks. Some of these include the use of complete Bayesian models updated through back-propagation [6], stochastic variational inference models [27] or mean field variational inference [51] as ways to update our knowledge of the data.
As a specific case of this, the Bayesian neural network (BNN) relies on the idea of Bayesian inference and attempts to model the weights, biases, outputs and other parameters as prob- ability distributions. BNNs operate as the variants of traditional deterministic deep learning methods that infer distributions over neural network models in a defined sample space. BNNs work by effectively sampling model instances to generate an output population, this makes them robust to over-fitting, offer significant uncertainty estimates, and can easily learn from small data sets. The benefit of these networks is that they operate considerably well with only a small amount of training data and are more resilient to over-fitting than typical artificial neural networks (ANNs). In practice, BNNs are able to signal a failure of prediction in multiple real-world scenarios including small embedded monitoring devices (on physical wearable devices), across physics domains such as black hole merges, autonomous driving, medical diagnostics or quantitative trading [35, 15, 37, 71].
Unlike conventional deterministic neural networks, BNNs introduce weight uncertainty by inducing probability distributions over weights of neural network models for uncertainty modelling, where each weight in the neural network follows a distribution instead of taking a fixed value. The goal of training is to infer the posterior distributions of weights $P(w|D)$ using Bayes’s rule, where w are the weights of our model and D is the set of input features, X, and labels, Y . Unfortunately, the computation of the normalising constant, $P(D)$, as described in Chapter 2 involves solving an intractable integral, $P (D|\theta)p(\theta)d\theta$. Alternatively variational inference [27] can be applied, which uses variational distributions $q(w|\theta)$ to approximate the posterior distribution $P(w|D)$. The alternative to variational distributions involves Markov chain Monte Carlo (MCMC) sampling which is unbiased but requires substantial computation.
There are strong reasons to support BNNs in the area of risk assessment of autonomous vehicles [5] to determine security risks for GPS spoofing attacks. Furthermore, with the work of Agamennoni et al. [1], there is substantial motivation to explore BNNs in this area to predict the behaviour of drivers in traffic. BNNs provide a level of managed failure, notifying of when it is unsure of what to predict and generalises better to new examples than other DNNs [14]. In comparison to CNNs for intelligent autonomous vehicles (IAVs), BNNs have the ability to work with missing data [40] such as broken sensors, uncertainty in random environments (such as a pedestrian appearing on the street) and predict probabilities of consequences given certain actions or evidence. All these approaches provide significant evidence for the use case of BNNs in not only IAVs but across a multitude of different domains.
The traditional method of Bayesian deep learning requires modelling uncertainty through the parameters of the models. Each weight in a BNN is governed by some distribution, usually in the case of stochastic variational inference, by restricting the posterior to a Gaussian parametric family. Although BNNs have shown considerable success in online learning tasks [50], their use in industry is tentative due to the number of parameters built into these models and their resultant hike in the required computational power. These two limitations also permeate to ensembling methods [38] where despite their excellent performance in accuracy and uncertainty quantification are potentially computationally infeasible for a variety of domains. More recent attempts have created novel solutions to the Bayesian deep learning problem with an aim to alleviate complexity through the treatment of hyperparameters as latent variables. Some approaches have used the hyperparameter of dropout, which is a regularisation term randomly dropping neurons in a network, or the depth of the network which is governed by the number of layers [18, 4]. Interestingly, these two methods resemble a paradigm shift of Bayesian neural networks, moving the generation of uncertainty from the weights themselves to other hyperparameters. Being able to accurately shift this representation of latent variables requires a sufficient depth or pool of combinations to satisfy reasonable uncertainty estimates.
As an alternative to designing specific hardware optimisations there is a strong attraction to simplify the over-parameterisation of models to deal with over-fitting and to create more robust solutions [28]. From this we can generate sparse models from our dense neural networks through two approaches, unstructured and structured sparsity. Unstructured sparsity, deals with the random dropping out of neurons, greatly reducing the number of parameters whilst maintaining similar levels of accuracy as its dense counterpart, yet being much more difficult to accelerate. Structured sparsity, although unable to match the accuracy of its unstructured counterpart is much more amenable to computational acceleration on GPU hardware such as PatDNN [49].
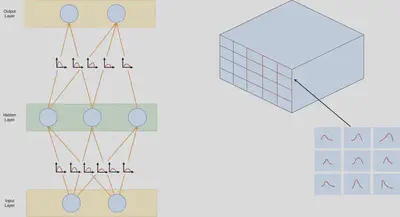
Combining these two aspects of state-of-the-art BNNs and sparse acceleration, our project proposes to represent a shift in the generation of uncertainty from the weights of our model to the probabilities of a pattern-based pruning approach. The notion behind this idea is that the pruning by these patterns introduces a robustness and flexible property to our model as the patterns modify the receptive fields of the kernels. Instead of having to deal with the excessive number of parameters which involves including both variance and mean into every single neuron weight, we propose reducing this excessive representation through a selection of pruning-patterns across the model’s kernels. Through the potential design of SpBNN, we can hopefully be able to extract an exponentially large number of possible model configurations by combining a small set of two-dimensional convolutional filter patterns. These filter patterns are known as kernel or channel groups and we would sample them to prune chunks of convolutional kernels that we call kernel/channel groups, saving memory and reducing computational costs.